TE2. Método de las Fuerzas para Estructuras Hiperestáticas

Método de las Fuerzas.

Los métodos la fuerzas, llamado también métodos de las flexibilidades o métodos de las deflexiones compatibles, ^JM son convenientes para el análisis de estructuras pequeñas, con unos cuantos elementos redundantes. ^AK Se suprimen un número suficiente de estas redundantes, de modo que se logre una estructura estáticamente determinada, ^JM o sea, la estructura por analizar se convierte en una estructura isostática en la que se satisfacen las condiciones de equilibrio. ^OC Se calculan los desplazamientos (lineales o angulares) en la dirección de las redundantes canceladas. Las redundantes deben ser de una magnitud tal que fuercen a sus puntos de aplicación a volver a su posición original de deflexión nula. Se establece una ecuación para la condición de deflexión en cada redundante y éstas se despejan de las ecuaciones resultantes. ^JM Estos métodos también se usan para deducir las relaciones de fuerza-deformación en los miembros, necesarias para desarrollar los métodos de los desplazamientos. 

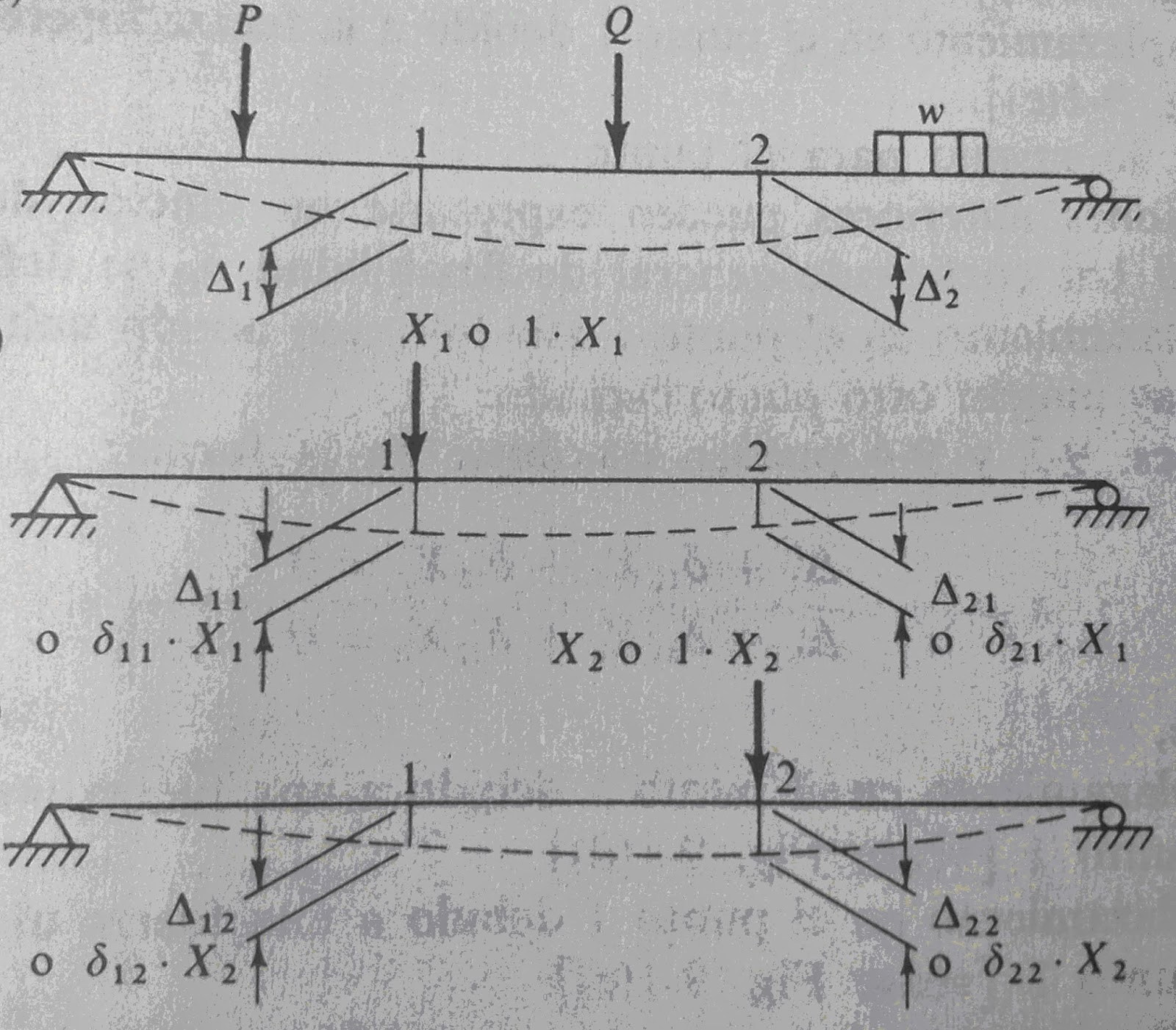
Considérese la viga continua sobre apoyos indeformables

Es estáticamente indeterminada de segundo grado, es decir, con dos redundantes. El primer paso en la aplicación del método es eliminar por ejemplo, los apoyos interiores e introducir en estos sitios las acciones hiperestáticas X₁ y X₂, respectivamente, consiguiendo de esta manera llevar la estructura a una condición de determinación y estabilidad. Dicha estructura se denomina estructura primaria.

 

En donde, con apoyos sin asentamientos, se encuentra que la compatibilidad requiere

Donde:

Desplazamiento en el punto 1.

Desplazamiento en el punto 2.

Utilizando el principio de superposición podemos poner las ecuaciones anteriores en la forma

 

Donde:

Desplazamiento en el punto 1 debido a las cargas externas.

Desplazamiento en el punto 1 debido a la Fuerza Hiperestática X₁.

Desplazamiento en el punto 1 debido a la Fuerza Hiperestática X₂.

Igual para las siguientes.

 

Las ecuaciones anteriores pueden expresarse en función de los coeficientes de flexibilidad*. Un coeficiente general de flexibilidadse define como el desplazamiento en el punto i debido a una acción unitaria en j, cuando no hay ningún otro punto cagado. Así, entonces las ecuaciones anteriores pueden escribirse en la forma

Evidentemente y por lo antes expuesto.

Desplazamiento en el punto 1 debido a la fuerza unitaria aplicada en el punto 1.

Desplazamiento en el punto 1 debido a la fuerza unitaria aplicada en el punto 2.

Tanto el desplazamiento producido por las cargas originales como los coeficientes de flexibilidad de la estructura primaria pueden obtenerse por cualquiera de los métodos para calcular deflexiones. Las hiperestáticas desconocidas se resuelven, pues, por medio del sistema de ecuaciones simultáneas. Este proceso puede generalizarse. Así, para una estructura con n hiperestáticas, se tiene

Planteamiento general del Método de las Fuerzas ^OG

Existen numerosas variantes en la aplicación del método, pero en todas ellas se distinguen los siguientes pasos:

a)  La estructura original Hiperestática se transforma en una estructura Isostática eliminando algunas de sus restricciones contra deflexiones o rotaciones. En general, el número de restricciones que hay que eliminar es igual al grado de indeterminación de la estructura. La estructura que resulta recibe el nombre de estructura isostática fundamental, o también estructura primaria.

b)     Se calculan las deformaciones de la estructura isostática fundamental bajo la acción de las mismas cargas que actúan en la estructura Hiperestática. Estas deformaciones se denominan incompatibilidades geométricas porque no existen en la estructura original en los puntos en los que se eliminaron las restricciones.

c)     Se aplican fuerzas arbitrarias en las secciones donde se eliminaron las restricciones y se calculan las deformaciones producidas por estas fuerzas correctivas. Es necesario aplicar una fuerza por cada restricción eliminada en la estructura hiperestática y calcular por separado las deformaciones debidas a cada fuerza. 

d)  Se plantea un sistema de ecuaciones para determinar el valor que deben tener las fuerzas correctivas de tal manera que se corrijan las incompatibilidades geométricas.

e)  Se obtienen las acciones finales (reacciones, fuerzas cortantes, fuerzas normales, momentos) sumando las que corresponden a la estructura isostática fundamental y las producidas por las fuerzas correctivas.

Nota del Profesor:

Las dudas e inquietudes serán discutidas en clases, igualmente pueden hacer uso de los comentarios. Recuerden que el Blog es una herramienta para el aprendizaje y la toma de apuntes correspondientes a las clases ya vistas o próximas a ver.

Referencias Bibliográficas:

McCormac, J. Análisis de Estructuras. Editorial Alfaomega.

González, O. (2009) Análisis Estructural. Editorial Limusa. 1° Ed.

Kassimali, A. (2001) Análisis Estructural. Editorial Thomsom Learning. 2° Ed.

Hsieh, Y. (1973) Teoría Elemental de Estructuras. Editorial Prentice/Hall International.  1° Ed.