Introducción a las Estructuras estáticamente Indeterminadas
Cuando una
estructura tiene mas reacciones externas o fuerzas internas que las que pueden
determinarse con las ecuaciones de la estática, tal estructura es estáticamente
indeterminada o Hiperestática. Una carga situada en alguna parte de una
estructura hiperestática o continua producirá fuerzas cortantes, momentos
flexionantes y deflexiones en las otras partes de la estructura. En otras palabras,
cargas aplicadas a una columna afectan a las vigas, a las losas, a otras
columnas y viceversa.
Es difícil
encontrar en la vida real vigas simplemente apoyadas, se puede decir lo mismo
de las armaduras, en un sentido estricto, todas éstas son realmente
estáticamente indeterminadas.
Ventajas de las estructuras Hiperestáticas
1. Esfuerzos
menores: en general, los esfuerzos
máximos en las estructuras estáticamente indeterminadas son menores que en las
estructuras determinadas. Considérese, los diagramas de momentos flexionantes
para las vigas mostradas, debido a una carga uniformemente distribuida, w
Fuente: Kassimali, Aslam. (2001)
Se
puede ver, a partir de las figuras mostradas, que el momento flexionante máximo
(y en consecuencia, el esfuerzo máximo de flexión) en la viga indeterminada es
significativamente inferior al de la determinada. AK
2. Ahorro de
materiales: por lo antes expuesto,
se permite la utilización de elementos de menor escuadría, con un ahorro de
material posiblemente del orden de 10
a 20% del acero utilizado en puentes, por ejemplo. JM
Un
elemento estructural de dimensiones dadas podrá soportar más carga si es parte
de una estructura continua, que si estuviera simplemente apoyada. La
continuidad permite el uso de elementos de menores dimensiones para las mismas
cargas y claros, o bien, un mayor espaciamiento de los apoyos para elementos de
iguales dimensiones. La posibilidad de utilizar menos columnas en edificios, un
menor número de pilares en el caso de puentes, puede ocasionar una reducción
global de los costos.
Las
estructuras de concreto armado de tipo monolítico se erigen de manera que son
naturalmente continuas y estáticamente indeterminadas. La instalación de
articulaciones y otro mecanismo de apoyo necesario para convertir tales sistemas
estructurales en isostáticos, no sólo presentarían difíciles problemas de
construcción sino que además elevaría bastante los costos. JM
3. Mayor rigidez
y menores deflexiones: en general,
las estructuras hiperestáticas son más rígidas que las isostáticas y sus
deflexiones o deformaciones son menores. Además, tienen mayor estabilidad
frente a todo tipo de cargas (horizontales, verticales, móviles, entre otras)
Según
el ejemplo anterior la deflexión máxima de la viga indeterminada sólo es la
quinta parte de la correspondiente a la determinada. JM. AK.
Viga Determinada Viga
Indeterminada
Fuente: Kassimali, Aslam. (2001)
4.
Redundancias: las estructuras hiperestáticas, si se diseñan en
forma apropiada, tienen la capacidad para redistribuir las cargas cuando
ciertas partes estructurales se llegan a reesforzar o se desploman en los casos
de sobrecarga debidas a temblores de tierra, tornados, impactos (por ejemplo
explosiones o choques de vehículos) y otros eventos. Las estructuras hiperestáticas
tienen más miembros o reacciones en los apoyos, o ambas características, que
los requeridos por la estabilidad estática, de modo que si una parte (o miembro
o apoyo) de esa estructura falla, la estructura completa no se desplomará
inevitablemente y las cargas se redistribuirán a las partes adyacentes de la
estructura.
Considere
las siguientes vigas
Suponga
que las vigas están sosteniendo un puente sobre una vía acuática y que se destruye
el pilar de en medio, B, cuando una
barcaza choca de manera accidental con él. En virtud de que la viga isostática
se encuentra apoyada en el número suficiente de reacciones requeridas para la
estabilidad estática, la eliminación del apoyo B, causará que la estructura completa se desplome como se muestra.
Sin
embargo la viga hiperestática tiene una reacción adicional en la dirección
vertical; por lo tanto, la estructura no se desplomará inevitablemente y puede
permanecer estable, incluso después que el apoyo B haya fallado.
Si
se supone que la viga ha sido diseñada para soportar sólo carga muerta, en el caso
de un accidente de este tipo, el puente se cerrará al tránsito hasta que se
repare el pilar B y después se
volverá a abrir. AK
5. Estructura más atractivas: es difícil imaginar a las estructuras isostáticas
con la belleza arquitectónica de muchos arcos y marcos rígidos hiperestáticos
que se construyen hoy día.
6. Adaptación al montaje en voladizo: el método de montaje en voladizo de puentes es de
gran valor cuando las condiciones en el sitio de erección (tráfico naval o niveles
muy profundos del agua) obstaculizan la erección de la obra falsa. Los puentes
continuos hiperestáticos y los de tipo en voladizo pueden erigirse
convenientemente con el método de montaje en voladizo. JM
Desventajas de las estructuras Hiperestáticas
1. Esfuerzos
debido a asentamiento en los apoyos:
los asentamientos de los apoyos no causan asentamientos en las estructuras isostáticas;
sin embargo pueden inducir esfuerzos significativos en las hiperestáticas. AK
Las estructuras hiperestáticas no son convenientes en todos aquellos casos donde
las condiciones de cimentación sean impropias, pues los asentamientos o ladeos
que se presenten en los apoyos de la estructura por leves que parezcan, pueden
causar cambios notables en los momentos flexionantes, fuerzas cortantes, esfuerzos
totales y reacciones. JM
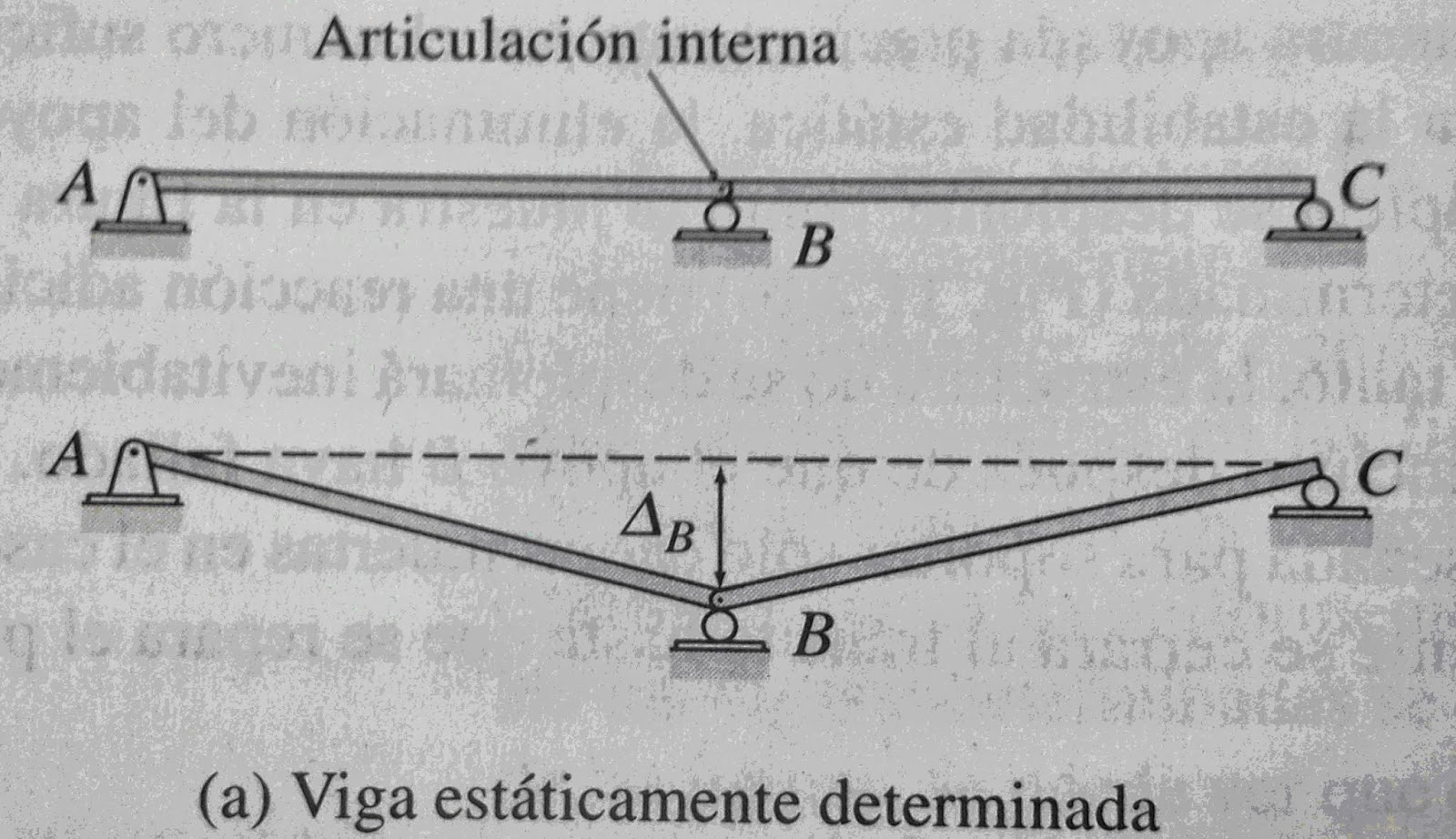
Considérense
las vigas isostáticas e hiperestáticas que se muestran.
En
la viga isostática el apoyo B sufre
un pequeño asentamiento, dB,
las partes AB y BC de esa viga, conectadas entre sí por una articulación interna en
B, se mueven como cuerpos rígidos,
sin flexionarse; es decir, permanecen rectos, no se desarrollan esfuerzos en la
viga isostática. Sin embargo cuando la viga indeterminada se sujeta a un
asentamiento similar del apoyo, se flexiona la viga, por tanto, se desarrollan
momentos flexionantes en la viga. AK
2. Aparición de otros esfuerzos: los cambios de la posición relativa de los
elementos estructurales causados por variación de temperatura, fabricación
deficiente o deformaciones internas por acción de la carga, pueden causar cambios
graves en la fuerzas en toda la estructura. JM
3. Dificultad de análisis y diseño: las fuerzas en las estructuras estáticamente
indeterminadas dependen no únicamente de sus dimensiones, sino también de sus
propiedades elástica (módulo de elasticidad, momentos de inercia, secciones
transversales, entre otros). Esta situación da lugar a una seria dificultad en
cuanto a su diseño: no podrán determinarse las fuerzas sino hasta conocer las
dimensiones de los elementos estructurales, y no podrán determinarse las
dimensiones sí no se conocen antes las fuerzas que actúan en ellos. El problema
se resuelve suponiendo las dimensiones de sus elementos y calculando las
fuerzas, diseñando los elementos para dichas fuerzas y evaluando las fuerzas
para las nuevas dimensiones supuestas y así sucesivamente, hasta lograr el
diseño final. El calculó mediante este procedimiento (métodos de aproximaciones
sucesivas) es más tardado que el que se requiere para diseñar una estructura isostática
similar, pero el costo adicional es una pequeña parte del costo total de la
estructura. Tales diseños se llevan mejor a cabo por medio de una interacción
con una computadora. JM
4. Inversión de las fuerzas: Generalmente en las estructuras hiperestáticas se
produce un mayor número de inversiones de fuerzas que en las estructuras isostáticas.
En ocasiones se requiere de más material de refuerzo en ciertas secciones de la
estructura, para resistir los diferentes estados de esfuerzos. JM
Métodos para analizar Estructuras Hiperestáticas.
Desde mediados
del siglo XIX, se han desarrollado muchos métodos para analizar las estructuras
hiperestáticas. Éstas pueden ser analizadas ya sea en forma "exacta"
o bien de modo "aproximado".
El análisis
exacto de las estructuras hiperestáticas comprende el cálculo de las
deflexiones y la resolución de ecuaciones simultáneas, depende además, de los
tamaños relativos de los miembros de la estructura. Debido a estas dificultades
asociadas con el análisis exacto, los diseños preliminares de las estructuras hiperestáticas
o indeterminadas a menudo se basan en los resultados de un análisis aproximado,
en el cual las fuerzas internas se estiman al establecer ciertas hipótesis
acerca de las deformaciones o la distribución de fuerzas entre los miembros de
las estructuras, o de ambas cosas, evitando de este modo la necesidad de
calcular las deflexiones. AK
Existen dos
métodos generales que estudian de forma "exacta" las estructuras
hiperestáticas, y se conocen como los métodos de las fuerzas y los métodos de
los desplazamientos.
En general, los
métodos la fuerzas, llamado también métodos de las flexibilidades o métodos de
las deflexiones compatibles, JM son convenientes para el análisis de
estructuras pequeñas, con unos cuantos elementos redundantes. AK Se
suprimen un número suficiente de estas redundantes, de modo que se logre una
estructura estáticamente determinada, JM o sea, la estructura por
analizar se convierte en una estructura isostática en la que se satisfacen las
condiciones de equilibrio.OG Se calculan los desplazamientos
(lineales o angulares) en la dirección de la redundantes canceladas. Las
redundantes deben ser de una magnitud tal que fuercen a sus puntos de
aplicación a volver a su posición original de deflexión nula. Se establece una
ecuación para la condición de deflexión en cada redundante y éstas se despejan
de las ecuaciones resultantes.JM Estos métodos también se usan para
deducir las relaciones de fuerza-deformación en los miembros, necesarias para
desarrollar los métodos de los desplazamientos.
Los métodos de
los desplazamientos, conocidos también como los métodos de las deformaciones o
de las rigideces,OG son más sistemáticos, se prefieren para
estructuras grandes e intensamente redundantes AK. En este
método de análisis se establecen ecuaciones con los desplazamientos de los
nudos (rotaciones y traslaciones) necesarios para describir completamente la
configuración deformada de la estructura, a diferencia de las ecuaciones del
método de las fuerzas que contienen acciones redundantes. Resolviendo las ecuaciones
simultáneas se encuentran esos desplazamientos que se sustituyen en las
ecuaciones originales para determinar las diversas fuerzas internas. JM
Nota del Profesor:
Las dudas e inquietudes serán
discutidas en clases, igualmente pueden hacer uso de los comentarios. Recuerden
que el Blog es una herramienta para el aprendizaje y la toma de apuntes correspondientes
a las clases ya vistas o próximas a ver.
Referencias Bibliográficas:
McCormac,
J. Análisis de Estructuras. Editorial Alfaomega.
González,
O. (2009) Análisis Estructural. Editorial Limusa. 1° Ed.
Kassimali,
A. (2001) Análisis Estructural. Editorial Thomsom Learning. 2° Ed.







No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.